How to Calculate a Mortgage Amortization Table

Amortization Formula and Spreadsheet for Schedule A Tax Deduction

I've written quite a bit about about how the interest payments on your mortgage can be deducted from your income tax, but only if they (and your other deductions) come to more than the standard deduction. In all cases, due to the existence of the standard deduction, you never get full value in exchange for the interest you are paying, just small fraction, depending on your tax bracket, etc. It's a deduction rather than a credit, though the government is talking about making it a better deduction (ie, not reducing it by the standard deduction in practice).

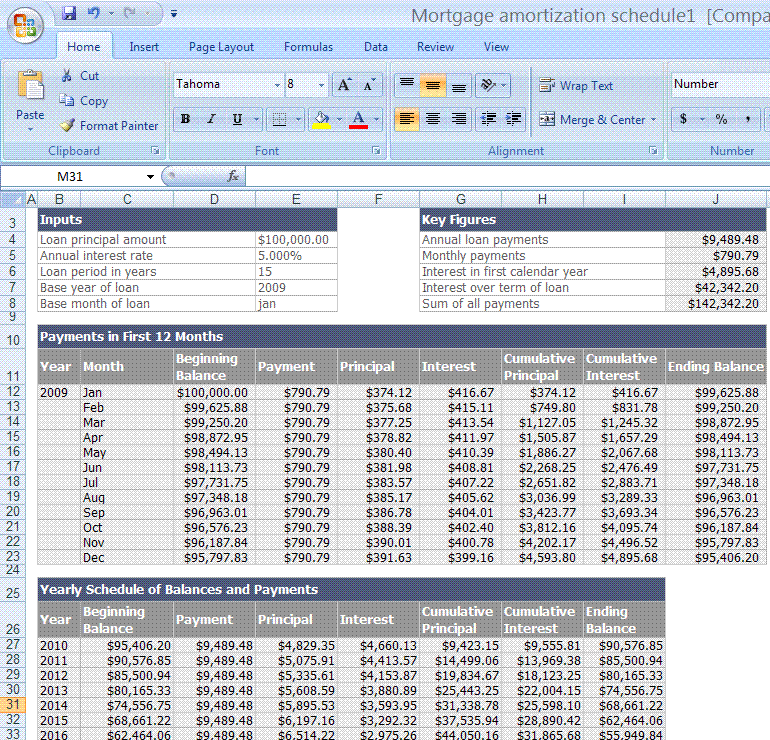
The formula for calculation of amortization tables is an iterative process, calculating the mortgage payment for a month, reducing the principal by a month's payment, calculating the interest paid that month. For example, using the fifteen year mortgage amount from my page on calculating interest to keep it simple, $100,000 at 5%, we get a monthly payment of $790.79 on a calculator with too many significant digits:-) So after one month, the outstanding balance is:

($100,000 - $790.79) + interest for the month

where the interest rate per month is 5% divided by 12 months, or .05/12 = 0.0041667, and the previous month principal is $100,000

so the interest for the month is $100,000 x .0041667 = $416.67

So, for the first month, the amount of principal paid on the loan is the monthly payment minus the interest that month or

$790.79 - $416.67 = $374.12

And the remaining principal amount is $100,000 - $374.12 = $99,625.88

Amortization Table Remaining Principal Principal Paid Interest Paid Total Interest Paid Total Principal Paid

End of Month 1 $99,625.88 $374.12 $416.67 $416.67 $374.12

To calculate a full mortgage amortization table, you would repeat the process for each month, reducing the principal by the amount paid down. Let's do one more month before we introduce the spreadsheet.

Interest paid 2nd month = $99,625.88 x .0041667 = $415.11

Principal paid 2nd month = $790.79 - $415.11 = $375.68

Remaining principal = $99,625.88 - $375.68 = $99,250.20

Total interest paid after two months is $416.67 + $415.11 = $831.78

Total principal paid after two months is $374.12 + $375.68 =

Updating our amortization table with a new line:

Amortization Table Remaining Principal Principal Paid Interest Paid Total Interest Paid Total Principal Paid

End of Month 1 $99,625.88 $374.12 $416.67 $416.67 $374.12

End of Month 2 $99,250.20 $375.68 $415.11 $831.78 $749.80

So can see how it's possible to calculate the amortization table for a mortgage in an afternoon, if you don't go batty first. They used to make us do this stuff in the numerical methods class I took in college - see how it works and only then do you get to use a computer. I actually got an "A" in that class. You could also sit down and just calculate enough of the cumulative interest each year (twelve iterations max) to do your taxes, which wouldn't take more than a half hour. Moving on to the computer, there's a nifty spreadsheet available free through Microsoft, I'll paste in the output below: